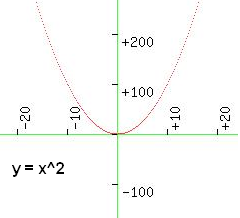
 Die einfachste Form der Parabel ist y = x^2 wie gezeichnet (Für jeden y-Wert Yp eines Punktes auf der Parabel [Xp,Yp] gilt, daß er
wertmäßig dem Produkt aus x mal x oder anders ausgedrückt dem Quadrat des x-Wertes Xp entspricht). Diese Parabel geht durch den Koordinatenursprung.
Die einfachste Form der Parabel ist y = x^2 wie gezeichnet (Für jeden y-Wert Yp eines Punktes auf der Parabel [Xp,Yp] gilt, daß er
wertmäßig dem Produkt aus x mal x oder anders ausgedrückt dem Quadrat des x-Wertes Xp entspricht). Diese Parabel geht durch den Koordinatenursprung.
Die Parabel ist bei Wikipedia allgemeiner als quadratisches Polynom erklärt.
(Stand: 06. Aug. 2008)