Allgemeines:

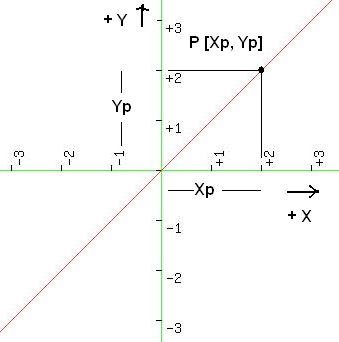
Das Koordinatenkreuz mit kartesischen Koordinaten

Achtung: es muß der Dezimalpunkt an Stelle des Komma eingegeben werden (0.75 anstelle von 0,75)!

Funktionsparameter
Wert von Xp (z.B.: 4)
Wert von Yp (z.B.: -36)

Maßstab festlegen
X-Skalierungswert (z.B.: 0.1, 0.02, 1, 150, usw.)
Y-Skalierungswert (z.B.: 0.01, 0.5, 100, 1500, usw.)

Lage des Koordinatenkreuzes festlegen
X0 in % der Bildbreite (von 0 bis 90)
Y0 in % der Bildhöhe (von 0 bis 90)



Grundlagen:

Koordinatenkreuz Ein Kartesisches Koordinatenkreuz besteht aus zwei senkrecht sich kreuzenden Geraden, die als Koordinatenachsen bezeichnet werden (im Bild in grüner Farbe gezeichnet). Die mit der x-Richtung versehene Achse zeigt für gewöhnlich nach rechts, die mit der y-Richtung bezeichnete Achse nach oben. Der Schnittpunkt der x- und y-Achse wird als Koordinatenursprung bezeichnet. Die Achsen erhalten Skalen in x- und y-Richtung, die im Ursprung jeweils mit dem Wert Null beginnen.
Ein Punkt im Kartesischen Koordinatenkreuz ist eindeutig in seiner relativen Lage zum Koordinatenursprung beschreibbar:
P = [Xp, Yp]. Dabei bedeutet verabredungsgemäß die X-Koordinate Xp die senkrechte Entfernung von der Y-Achse auf der X-Achse gemessen (+ nach rechts, - nach links). Die Y-Koordinate Yp wird analog auf der Y-Achse abgelesen (+ nach oben, - nach unten). Der Koordinatenursprung ist also z.B. P[X0, Y0] oder auch M[0, 0] - die Punktbezeichnung mit Buchstaben ist frei wählbar.
Wenn beliebige Koordinatenpaare [Xp, Yp] (das sind darstellbare Punkte) in einen berechenbaren Zusammenhang gebracht werden (Formel, Gleichung), so entstehen beim Zeichnen aller Punkte Figuren wie z.B. Geraden oder Parabeln. Die einfachste Form ist die Nullpunktgerade: y = x wie in roter Farbe gezeichnet. Für jeden Y-Wert (Yp) gilt, daß er wertmäßig dem X-Wert (Xp) entspricht.

Das kartesische Koordinatensystem ist bei Wikipedia ausführlicher erklärt, auch dass es weitere Koordinatensysteme gibt.


(Stand: 06. Aug. 2008)