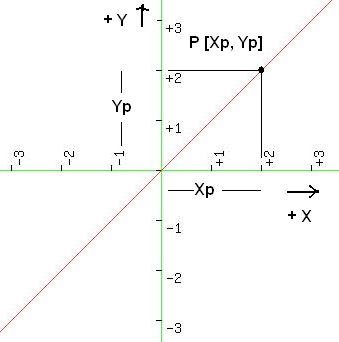
 Die einfachste Form der Geradengleichung ist y = x wie gezeichnet (Für jeden y-Wert Yp gilt, daß er wertmäßig dem x-Wert Xp entspricht). Das Verhältnis der y-Koordinate zur x-Koordinate beliebiger Punkte P[Xp,Yp] auf der Geraden ist konstant und für den Fall Xp=Yp natürlich =1!
Dieser Geradentyp heißt Nullpunktgerade:
Die einfachste Form der Geradengleichung ist y = x wie gezeichnet (Für jeden y-Wert Yp gilt, daß er wertmäßig dem x-Wert Xp entspricht). Das Verhältnis der y-Koordinate zur x-Koordinate beliebiger Punkte P[Xp,Yp] auf der Geraden ist konstant und für den Fall Xp=Yp natürlich =1!
Dieser Geradentyp heißt Nullpunktgerade:Die Geradengleichung ist bei Wikipedia ausführlicher erklärt.
(Stand: 06. Aug. 2008)