Allgemeines:

Der Kreis in der Form y^2 + x^2 = 1

Achtung: es muß der Dezimalpunkt an Stelle des Komma eingegeben werden (0.75 anstelle von 0,75)!

Funktionsparameter
(z.B.: .6)
Mittelpunkt Xm = 0
Mittelpunkt Ym = 0
Xp von P(Xp,+Yp) auf Kreis

Maßstab festlegen
X- und Y-Skalierungswert (z.B.: 0.1, 0.02, 1, 150, usw.)

Lage des Koordinatenkreuzes festlegen
X0 in % der Bildbreite (von 0 bis 50)
Y0 in % der Bildhöhe (von 0 bis 50)


Grundlagen

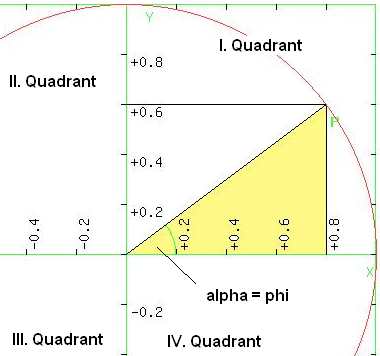
Einheitskreis Die allgemeine Kreisgleichung eines Kreises um den Koordinatennullpunkt ist x^2 + y^2 = r^2. Dabei ist r der Radius des Kreises. Wird der Radius auf den Wert 1 gesetzt, so handelt es sich um den sog. Einheitskreis. Löse ich die Gleichung nach y auf, so ergibt sich für den x-Bereich -r <= x <= +r: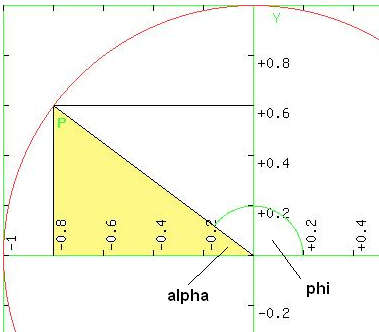
y = +- sqrt(1 - x^2)
Die Abkürzung sqrt steht für 'Wurzel aus'. Es gibt also zwei y-Werte zu einem x-Wert! Wenn ich den Mittelpunkt M = [Xm, Ym] vom Koordinatenursprung weg verschieben will, setze ich in der Kreisgleichung für X --> (X - Xm) und für Y --> (Y - Ym).

Der Einheitskreis verdeutlicht anschaulich, was mit den trigonometrischen Funktionen gemeint ist, bzw. wie sie definiert sind. Der Radius und der zugehörige x- und y-Wert (für auf dem Kreis gelegene Punkte) bilden ein rechtwinkliges (gelbes) Dreieck mit dem Winkel alpha zwischen x-Achse (Ankathete) und Radius (Hypotenuse) im Inneren des Dreiecks.

Ein charakteristischer Wert für den Winkel phi gebildet zwischen dem Radius und der x-Achse sind die verschiedenen Seitenverhältnisse (Quotienten) im genannten Dreieck (wegen Radius r=1 ist Yp/r = Yp). Der Winkel phi soll dabei von der x-Achse beginnend (0 Grad) entgegen dem Uhrzeigersinn größer werden. Im ersten Quadranten entspricht phi dem Dreieckswinkel alpha und es gelten die Definitionen:
Einheitskreis Yp = sin(phi),
Xp = cos(phi) und
Yp/Xp = tan(phi).

Auch ist sofort klar, dass Yp/Xp = sin(phi) / cos(phi) sein muss, die hierfür gewählte Bezeichnung ist tan(phi).
Damit ist der Definition entsprechend ablesbar, dass Winkel im ersten und zweiten Quadranten einen positiven sinus-Wert haben, im dritten und vierten Quadranten einen negativen Wert (jeweils die y-Koordinate). Die cosinus-Werte jedoch im ersten Quadranten positiv, im zweiten negativ, im dritten negativ und im vierten Quadranten wieder positiv sein müssen (jeweils die x-Koordinate). Die Winkelfunktionen wiederholen sich alle 360 Grad, sie sind periodisch: sin(phi) = sin(phi + n*360), wobei n ganze Zahlen sind.

Die Kreisgleichung ist bei Wikipedia nachzulesen, die trigonometrische Sicht auf den Einheitskreis ebenfalls.


(Stand: 06. Aug. 2008)