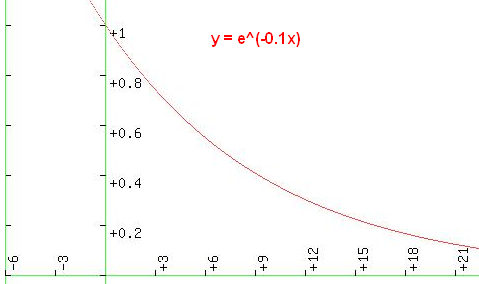
 y = e^(-0.1x) ist die nebenstehend abgebildete e-Funktion. Du kannst Dir vorstellen, daß eine beliebige andere Funktion, multipliziert mit dieser e-Funktion (y-Werte werden multipliziert), eine neue Funktion ergibt, bei der mit steigenden x-Werten eine ständige Verkleinerung der neuen Funktion in den y-Werten zu sehen sein wird.
y = e^(-0.1x) ist die nebenstehend abgebildete e-Funktion. Du kannst Dir vorstellen, daß eine beliebige andere Funktion, multipliziert mit dieser e-Funktion (y-Werte werden multipliziert), eine neue Funktion ergibt, bei der mit steigenden x-Werten eine ständige Verkleinerung der neuen Funktion in den y-Werten zu sehen sein wird.
(Stand: 06. Aug. 2008)