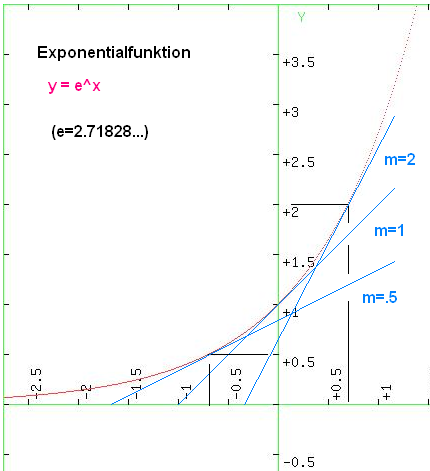
 Eine der wichtigsten natürlich gegebenen "Zahlen" ist die Eulersche Zahl e, in Wikipedia ausfühlich beschrieben. Eine besondere Funktion damit ist die e-Funktion (Exponentialfunktion) y=e^x.
Eine der wichtigsten natürlich gegebenen "Zahlen" ist die Eulersche Zahl e, in Wikipedia ausfühlich beschrieben. Eine besondere Funktion damit ist die e-Funktion (Exponentialfunktion) y=e^x. Die Bedeutung der Exponentialfunktion kannst Du bei Wikipedia erahnen.
(Stand: 06. Aug. 2008)