Allgemeines:

Kosinus in der Form y = m*cos(x) + n

Achtung: es muß der Dezimalpunkt an Stelle des Komma eingegeben werden (0.75 anstelle von 0,75)!

Funktionsparameter
Wert von m (z.B.: -1)
Wert von n (z.B.: .5)

Maßstab festlegen
X-Skalierungswert (z.B.: 3.14, 0.8)
Y-Skalierungswert (z.B.: 0.2, 0.5)

Lage des Koordinatenkreuzes festlegen
X0 in % der Bildbreite (von 0 bis 90)
Y0 in % der Bildhöhe (von 0 bis 90)



Grundlagen

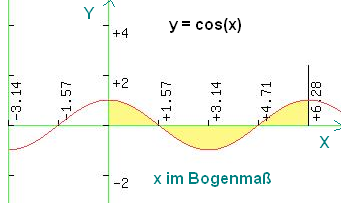
Cosinusfunktion Die Kosinus-Funktion gehört zu den trigonometrischen Funktionen. Ihre Definition kann am Einheitskreis nachvollzogen werden. In der Abbildung ist eine Periode gelb unterlegt. Gegenüber der Sinusfunktion sind die Funktionswerte um 90 Grad verschoben!

Wenn bei Schwingungsdarstellung die x-Achse der Zeit und die y-Achse z.B. der Auslenkung eines Pendels entspricht, so ist 1 geteilt durch die Periodendauer die Frequenz der Schwingung in Hertz.

In der Programmiersprache PHP wird in der Kosinusfunktion für den Winkel das Bogenmaß als Parameter erwartet. Der Einfachheit halber habe ich keine Umrechnungen vorgenommen, so dass die Grafik auf der x-Achse im Bogenmaß vorgegeben ist. Die Umrechnung Bogenmaß in Grad und umgekehrt erfolgt nach den Gleichungen (Pi~3.14):
Bogen im Bogenmaß = 2 * Pi * (Gradzahl/360)
Gradzahl = 360 * (Bogen im Bogenmaß / (2 * Pi) ).
(Was fällt auf? Der Umfang eines Kreises ist 2*Pi*Radius, der des Einheitkreises ist 2*Pi=6.28 entsprechend dem Bogen eines Vollkreises - entsprechend einer vollen Schwingungsdauer beim Kosinus!)
Wenn Du m variierst, erhälst Du gestreckte oder gestauchte Funktionswerte, bei negativem m eine Spiegelung an der Mittelachse.
Der Parameter n verschiebt die Kurve nach oben oder unten.

Die Kosinusfunktion ist bei Wikipedia entsprechend erklärt. Auch hier erfolgt der Hinweis auf den Einheitskreis.


(Stand: 06. Aug. 2008)